Architecture
Votre complexe d'appartements doit comporter un certain nombre d'étages, dans lesquels se trouveront un certain nombre d'appartements. Il est vital que:
- Chaque étage soit composé d'une seule rangée d'appartements connexes. Avoir des sections non-connexes sur un étage serait d'un style années 90 les plus rétrogrades.
- Au moins un appartement sur chaque étage doit reposer sur un appartement de l'étage inférieur, sauf l'étage du bas qui doit reposer sur le sol.
Quelques exemples d'immeubles valides et invalides sont montrés sur le schéma ci-dessous. Les immeubles de gauche suivent les règles indiquées plus haut. Les trois immeubles de droite sont invalides : dans le premier immeuble, le troisième étage contient deux sections non-connexes, dans le deuxième immeuble, le troisième étage ne repose pas sur le second, et dans le dernier immeuble, l'étage inférieur ne touche pas le sol.

Malheureusement, votre génie créatif incomparable est bridé par des contraintes purement commerciales: les appartements ne peuvent être vendus s'ils n'ont pas la meilleure vue possible. Pour chaque point de l'espace, vous disposez d'un nombre indiquant à quel point la vue y est splendide. Étant donné un nombre d'appartements N, votre objectif est de concevoir un immeuble comportant exactement N appartements et tel que la somme des qualités de vue pour les N appartements soit aussi grande que possible.
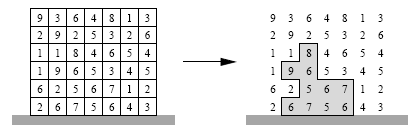
Par exemple, considérez la grille située à gauche du schéma ci-dessus. Elle indique les qualités de vue pour un terrain, la ligne du bas contenant les scores des appartements du rez-de-chaussée, la deuxième ligne ceux du premier étage, etc.
Supposez qu'on vous ait demandé de concevoir un immeuble contenant N=10 appartements. La partie de droite du schéma contient un exemple d'immeuble qui convient. La somme de ses qualités de vue est 8+9+6+5+6+7+6+7+5+6 = 65. On peut montrer qu'il s'agit du meilleur immeuble que vous pouvez concevoir, c'est-à-dire que vous ne pouvez concevoir aucun immeuble ayant un score total supérieur à 65.
LAIKO IR ATMINTIES RIBOJIMAI (Python)
- Laiko ribojimas: 5 sek., procesorius: 1GHz.
- Atmintis: 32,000 KB.
RIBOJIMAI
- 1 <= N <= 80, où N est le nombre d'appartements dans votre immeuble;
- 1 <= W, H <= 80, où la grille des qualités de vue est de largeur W et de hauteur H;
- Il est possible de construire un immeuble ayant N appartements, c'est-à-dire que l'on a N <= WxH.
De plus, pour 30% des immeubles à concevoir, l'entrée satisfera 1 <= N, W, H <= 20.
PRADINIAI DUOMENYS
La deuxième ligne de l'entrée contiendra les entiers W et H, séparés par un espace: les dimensions de la grille de nombres.
Les H lignes suivantes contiendront chacune W entiers séparés par des espaces: les qualités de vue pour les différents points de l'espace. La dernière ligne de l'entrée contient les qualités de vue du rez-de-chaussée, l'avant-dernière ligne ceux du premier étage, etc. Toutes les qualités de vue seront comprises entre 1 et 100 000 inclus.
REZULTATAI
PAVYZDYS
pradiniai duomenys:
10 7 6 9 3 6 4 8 1 3 2 9 2 5 3 2 6 1 1 8 4 6 5 4 1 9 6 5 3 4 5 6 2 5 6 7 1 2 2 6 7 5 6 4 3
rezultatai:
65