Jackpot
|
Lors d'un séjour à Las-Vegas, vous vous balladez dans les allées d'un casino, observant avec curiosité les très nombreux joueurs assis devant les machines à sous qui, tels des automates, exécutent une routine toujours identique : insérer une pièce, tirer le levier, regarder les roues tourner, attendre le résultat, insérer une pièce, tirer le levier, etc. Certains essaient d'augmenter leurs chances de gains, par exemple en soufflant sur leur pièce avant de l'insérer, sans compter les nombreux grigris, fers à cheval et autres porte-bonheur. Vous êtes convaincu qu'aucune de ces techniques n'a le moindre effet sur le résultat. |  |
Après de nombreuses heures d'observation, vous commencez à comprendre la manière dont ces machines infernales fonctionnent, et réalisez qu'il est en fait possible de jouer d'une manière qui augmente vos chances de gain. En effet, sur le modèle de machines à sous de ce casino, les chances de gains au prochain coup varient suivant la configuration initiale de ses roues ! Si ceci ne permet en rien d'influencer le résultat pour une machine donnée, vous pouvez choisir à chaque tour, de jouer sur la machine qui a le plus de chances de remporter le jackpot !
Une machine à sous est composée de N roues. Sur chacune des roues sont représentés S symboles que l'on identifiera par des entiers. Lorsque l'on abaisse le levier, une quantité d'énergie E bien précise est répartie aléatoirement entre les différentes roues. Chaque unité d'énergie transmise à une roue la fait tourner d'un cran, toujours dans le même sens, faisant apparaître le symbole suivant dans la fenêtre affichant le résultat. La somme des énergies transmises aux N roues est toujours exactement égale à E.
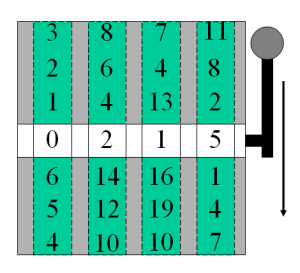
Vous devez écrire un programme qui détermine, pour une configuration initiale donnée d'une machine à sous, quel est le meilleur score que vous pouvez espérer obtenir au prochain tour, c'est-à-dire le nombre maximal de symboles identiques qui peuvent être alignés sur la fenêtre centrale, une fois que l'ensemble de l'énergie disponible a été dépensée pour faire tourner les diverses roues.
Limites de temps et de mémoire (Python)
- Temps : 2 s sur une machine à 1 GHz.
- Mémoire : 64 000 ko.
Contraintes
- 1 <= N <= 1000, où N est le nombre de roues de la machine à sous.
- 1 <= S <= 1000, où S est le nombre de symboles (tous distincts) présents sur une roue.
- 0 <= V <= 1 000 000, où V est l'identifiant numérique représentant un symbole présent sur une roue.
- 0 <= E <= 100 000 000, où E est l'énergie répartie aléatoirement entre les roues lorsque l'on actionne la machine.
- dans 40% des tests au total, N <= 75, S <= 75 et V <= 1 000.
- dans 20% autres tests, on a toujours N <= 75 et S <= 75, mais V <= 100 000.
Entrée
Chacune des N lignes suivantes contient S entiers séparés par des espaces, décrivant les identifiants des symboles présents sur une roue, dans l'ordre dans lesquels ils défilent, et en commençant par celui qui apparaît sur la zone du résultat dans la configuration initiale.
Sortie
Exemple
entrée :
4 7 11 0 1 2 3 4 5 6 2 4 6 8 10 12 14 1 13 4 7 10 19 16 5 2 8 11 7 4 1
sortie :
3
Commentaires
L'état initial correspond à l'illustration fournie dans le problème. On le représente ci-dessous avec les roues horizontales, et la fenêtre à gauche, pour faire facilement le lien avec l'entrée. Une unité d'énergie fait toujours tourner une roue vers la gauche, la fenêtre du résultat étant toujours la colonne de gauche.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 4 | 6 | 8 | 10 | 12 | 14 |
| 1 | 13 | 4 | 7 | 10 | 19 | 16 |
| 5 | 2 | 8 | 11 | 7 | 4 | 1 |
Si l'on a de la chance, l'énergie peut être répartie de telle sorte que trois symboles identiques soient alignés. En effet, si 2 unités d'énergie sont affectés à la première roue, 0 à la deuxième, 1 à la quatrième, et les 8 qui restent à la troisième, on obtient la configuration suivante, en ayant dépensé exactement les 11 unités d'énergie :
| 2 | 3 | 4 | 5 | 6 | 0 | 1 |
| 2 | 4 | 6 | 8 | 10 | 12 | 14 |
| 13 | 4 | 7 | 10 | 19 | 16 | 1 |
| 2 | 8 | 11 | 7 | 4 | 1 | 5 |
On se retrouve avec trois fois le symbole "2" dans la zone du résultat.
Une autre possibilité est que les symboles "1" soient alignés : en partant de la configuration initiale, si 1 unité d'énergie est affectée à la première roue, 4 à la deuxième, 0 à la troisième et 6 à la quatrième, on obtient la situation suivante :
| 1 | 2 | 3 | 4 | 5 | 6 | 0 |
| 10 | 12 | 14 | 2 | 4 | 6 | 8 |
| 1 | 13 | 4 | 7 | 10 | 19 | 16 |
| 1 | 5 | 2 | 8 | 11 | 7 | 4 |
Il n'est par contre pas possible d'aligner 4 symboles identiques. Le seul symbole qui soit sur les 4 roues est le symbole 4, et il faudrait 12 points d'énergie au minimum pour atteindre la configuration correspondante. Notez qu'on peut d'ailleurs également l'obtenir avec 19 points, 26, etc : il est possible de faire faire plusieurs tours à une même roue.
Squelette de code C++ :
#include <cstdio>
#include <cstdlib>
using namespace std;
int main()
{
int nbRoues, nbSymboles, energie;
scanf("%d%d%d", &nbRoues, &nbSymboles, &energie);
for (int roue = 0; roue < nbRoues; roue++)
{
for (int cran = 0; cran < nbSymboles; cran++)
{
int symbole;
scanf("%d", &symbole);
// ...
}
}
int maxAlignes; // ...
printf("%d\n", maxAlignes);
}
Squelette de code Caml :
let scan_int () = Scanf.scanf " %d" (fun x -> x)
let nbRoues = scan_int()
let nbSymboles = scan_int()
let energie = scan_int()
let etat =
Array.init nbRoues (fun _ ->
Array.init nbSymboles (fun _ ->
scan_int()))
(* "etat" est une matrice représentant l'état initial.
"etat.(id_roue).(cran)" contient ainsi la valeur du symbol
qui se trouve sur la machine sur la roue "id_roue" au cran
"cran". *)
let _ =
let maxAlignes = 0 (* compléter ici *) in
Printf.printf "%d\n" maxAlignes