La clôture d'Alice
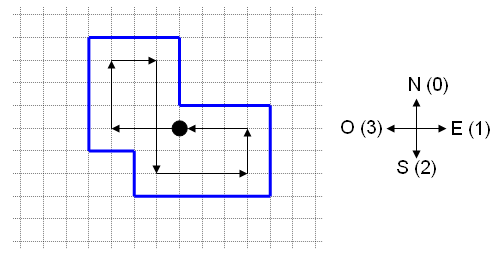
On vous donne la description du parcours de Bob, qui commence et se termine au même endroit (sa niche), sous la forme d'une succession de déplacements. Pour chaque déplacement, on indique la direction dans laquelle il se déplace, et la distance en mètres qu'il parcourt dans cette direction. Sachant que la clôture doit être constituée uniquement de segments parallèles aux axes Nord-Sud et Est-Ouest, et qu'Alice souhaite laisser au minimum un mètre entre le chien et la clôture, déterminer la longueur minimale de clôture qu'elle doit utiliser pour entourer entièrement le parcours de Bob.
LIMITES DE TIEMPO Y MEMORIA (Python)
- Tiempo: 1s sobre una máquina de 1GHz.
- Memoria: 4,000 Kb.
RESTRICCIONES
- 2 <= N <= 10 000, où N est le nombre de déplacements du parcours de Bob,
- 1 <= Li <= 100, où D est la longueur d'un déplacement de Bob.
ENTRADA
Chacune des N lignes suivantes décrit un déplacement du parcours de Bob. Chaque ligne est composée de deux entiers séparés par un espace : Di, la direction du déplacement (0 pour Nord, 1 pour Est, 2 pour Sud, 3 pour Ouest), et Li, la longueur du déplacement.
SALIDA
EJEMPLO
entrada:
7 3 3 0 3 1 2 2 5 1 4 0 2 3 3
salida:
30
COMENTARIOS
#include <cstdio>
int main()
{
int nbEtapes;
scanf( "%d", &nbEtapes);
// ....
for(int etape = 0 ; etape < nbEtapes ; etape++)
{
int direction, distance;
scanf("%d %d", &direction, &distance);
// ....
}
printf("%d\n", votre solution);
return 0;
}
Exemple de code pour lire l'entrée en OCaml :
let scan_int () = Scanf.scanf " %d" (fun x -> x)
let show_int n = Printf.printf "%d\n" n
let _ =
let nbEtapes = scan_int() in
(* ... *)
for etape = 0 to nbEtapes - 1 do
let direction = scan_int() in
let distance = scan_int() in
(* ... *)
done;
show_int (votre solution);
Deux conseils sont disponibles pour ce sujet. Utilisez-les si vous ne voyez pas comment le résoudre. Chaque conseil coûte 15 points.