Ce document est une synthèse de deux nouvelles structures de données : le tableau cumulatif 2D et la combinaison du tableau trié et de la dichotomie.

Outre un rappel des principes de chaque strucutre de données, un modèle de code est présenté pour chaque structure.

Surtout, les différentes utilisations classiques de chaque structure sont présentées. Ce dernier point ne doit pas à être négligé : même si ces structures sont simples, penser à les utiliser lorsque c'est approprié peut être la clé de la résolution d'exercices de haut niveau.

Tableau cumulatif 2D

Le tableau cumulatif 2D est une généralisation à deux dimensions du tableau cumulatif : on dispose d'un tableau à deux dimensions contenant diverses valeurs, et on effectue régulièrement des requêtes de type "quelle est la somme des valeurs contenues dans tel rectangle ?".

Comme dans la version 1D, on va précalculer un certain nombre de valeurs, mais cette fois dans un tableau cumulatif à deux dimensions. Aux coordonnées (lig,col) du tableau cumulatif, on va stocker la somme des valeurs se trouvant strictement au dessus et à gauche de la position correspondante dans le tableau des valeurs fournies (en supposant que la case (0,0) soit en haut à gauche).

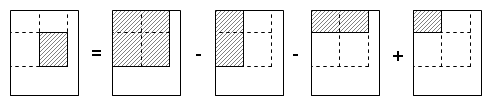
Pour une requête donnée, sur un rectangle défini par ses coins haut gauche [lig1, col1], et bas droit [lig2, bas2] (exclu), la somme des valeurs au sein de ce rectangle peut être obtenue par la formule suivante :

sommeRectangle(lig1, col1, lig2, col2) = sommeAvant(lig2, col2) - sommeAvant(lig2, col1)
                                       - sommeAvant(lig1, col2) + sommeAvant(lig1, col1)

Remplissage du tableau :

sommeAvant[NB_LIGS + 1][NB_COLS + 1]; // initialisé à 0
valeurs[NB_LIG][NB_COLS]; // données lues en entrée

for (int lig = 0; lig < nbLignes; lig++)
{
   int sommeLigne = 0;
   for (int col = 0; col < nbCols; col++)
   {
      sommeLigne += valeurs[lig][col];
      sommeAvant[lig + 1][col + 1] = sommeAvant[lig][col + 1] + sommeLigne;
   }
}

Il est important de noter que le tableau sur lequel on effectue les requêtes n'est pas toujours présenté clairement comme un tableau à deux dimensions dans le sujet. Les deux dimensions utilisées correspondent parfois à deux propriétés bien distinctes des objets sur lesquels on travaille. Une dimension pourra par exemple être une position, et l'autre le temps.

Tableau trié et dichotomie

Tier les objets contenus dans un tableau selon une propriété permet d'effectuer diverses opérations bien plus rapidement qu'avec un tableau non trié. Le critère choisi pour le tri dépendra bien sûr des spécificités des opérations à effectuer.

Pseudo-code du tri en C++

On utilise la fonction sort de la STL, et on définit l'ordre de tri en redéfinissant l'opérateur < des objets à trier. Exemple en triant par ordre croissant :

#include <algorithm>
using namespace std;

struct Objet
{
   int critere;

   bool operator < (const Objet& autre) const
   {
      return critere < autre.critere;
   }
};

Objet objets[NB_OBJETS]

sort(objets, objets + nbObjets);

Si l'on souhaite trier selon un deuxième critère, ou si l'on veut trier des données d'un type de base selon un ordre non standard, on crée une structure spécifique pour définir l'ordre de tri, dans laquelle on redéfinit l'opérateur ().

Exemple où l'on trie par critère décroissant :

#include <algorithm>
using namespace std;

Objet objets[NB_OBJETS]

struct CritereDecroissant
{
   bool operator() (Objet a, Objet b) const
   {
      return a.critere > b.critere;
   }
};

sort(objets, objets + nbObjets, CritereDecroissant());

Une fois que l'on dispose d'un tableau trié, on peut rechercher rapidement des objets au sein de ce tableau à partir de la valeur de leur critère, en utilisant une dichotomie.

TODO : fin de la section sur la dichotomie