Gardes

C'est l'heure des Olympiades annuelles de lancer de Boomerang et de Croissant, et les hôtes ont dépensé sans compter. Une grande partie de la ville a été bouclée entièrement pour accueillir les athlètes et les journalistes, sans oublier les responsables des barbecues et les chefs pâtissiers Français. Avec toute cette agitation, vous vous êtes retrouvés responsable de la sécurité de l'événement.

Chaque route qui arrive dans la zone réservée à l'Olympiade a été condamnée, pour assurer qu'il n'y ait pas d'intrus indésirables. Cependant, les hôtes ont dépensé tellement pour les cérémonies d'ouverture et de clôture qu'il ne reste plus assez d'argent pour embaucher assez de gardes de sécurité. Votre but est d'embaucher aussi peu de gardes que possible, tout en garantissant la sécurité de la zone.

La zone des Olympiades peut être vue comme une grande région circulaire, avec des routes qui arrivent à différents points du contour. Le gouvernement requiert que tout point où une route entre dans la zone soit au maximum à K mètres d'un agent de sécurité, la distance étant mesurée le long du cercle. Les gardes ne peuvent être placés que là où arrivent des routes, ils ne peuvent jamais se trouver dans les zones se trouvant entre ces positions.

Un exemple est donné dans le diagramme ci-dessous. Sept routes arrivent dans la zone, les distances entre-elles étant indiquées sur le diagramme. Supposez que le gouvernement ait déclaré que K=30. Dans ce cas, en plaçant trois gardes aux routes marquées par des étoiles, vous pouvez vous assurer que toute route est gardée.

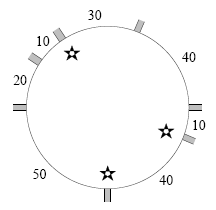
Votre objectif est, étant donné les distances entre les routes et la valeur de K, de déterminer le plus petit nombre de gardes nécessaire.

Limites de temps et de mémoire (Python)

  • Temps : 3 s sur une machine à 1 GHz.
  • Mémoire : 30 000 ko.

Contraintes

  • 1 <= N <= 1 000 000, où N est le nombre de routes qui arrivent sur la zone des Olympiades;
  • 1 <= D <= 1 000, où D est la distance entre deux routes adjacentes;
  • 1 <= K <= 10 000 000, où K est la valeur donnée par le gouvernement, comme décrit plus haut.

De plus, 30% des points attribués sont consacrés à des tests pour lesquels le nombre de routes satisfait 1 <= N <= 1 000.

Entrée

Votre programme doit lire sur l'entrée standard. La première ligne contiendra les entiers N et K, séparés par un espace, comme décrit plus haut.

Les N lignes suivantes décrivent chacune la distance entre deux routes adjacentes. Ces distances seront données dans l'ordre de parcours autour du cercle.

Plus précisément, supposons que les routes sont numérotées 1,2,...,N dans l'ordre des aiguilles d'une montre autour du cercle. Alors la ième de ces lignes sera la distance, selon l'ordre des aiguilles d'une montre, entre la ième et la i+1ème route, la Nème ligne donnant la distance entre la Nème et la première route.

Sortie

Votre programme doit afficher une seule ligne sur la sortie standard. Cette ligne doit contenir un simple entier, qui donne le plus petit nombre d'agents de sécurité requis.

Exemple

entrée : 

7 30
30
40
10
40
50
20
10

sortie : 

3

Commentaires

Calcul du score

Le score pour chaque test d'entrée sera de 100% si la bonne réponse est affichée, et de 0% sinon.

Source : https://www.france-ioi.org/