La division entière

On souhaite effectuer la division de 3395 par 99. Vous avez appris il y a fort longtemps à poser cette division à la main, ce qui donne la chose suivante :

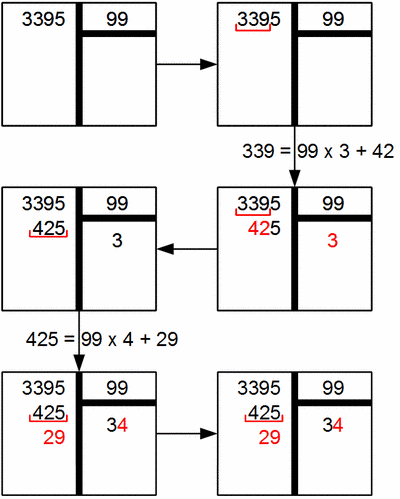
On s'est arrêté car 29 est plus petit que 99 et qu'on ne souhaitait pas aller plus loin et se retrouver avec un nombre à virgule. On a effectué une division dite division entière. On en déduit donc que 3395 = 99 * 34 + 29

Une fois cette division posée, on peut définir les 4 termes dividende, diviseur, quotient, reste, représentés sur le schéma suivant :

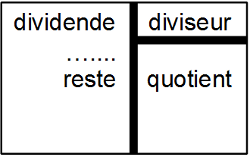
Le reste est donc ici 29 et le quotient est 34.

Multiple et diviseur

On a donc dividende = diviseur x quotient + reste.

Que se passe-t-il si le reste est égal à 0, par exemple dans la division entière de 1287 par 99 où on a 1287 = 99 * 13 + 0 ?

On dit alors que 99 est un diviseur de 1287 et que 1287 est un multiple de 99.

Les multiples de 99 sont tous les nombres qui peuvent s'écrire sous la forme "99 x n" avec "n" un nombre entier. Ainsi, les multiples de 99 sont 0, 99, 198, 297, 396, 495, 594, 693, 792, 891...

De manière intuitive, un nombre "d" est diviseur d'un nombre "n" s'il est possible de couper "n" en "d" paquets de taille égale. Dans l'exemple précédent, on a coupé 1287 en 99 paquets de taille 13, donc 99 était un diviseur de 1287.

Un nombre a généralement plusieurs diviseurs (seul le nombre 1 n'en a qu'un seul, lui-même), par exemple le nombre 420 a 24 diviseurs : 1, 2, 3, 4, 5, 6, 7, 10, 12, 14,15, 20, 21, 28, 30, 35, 42, 60, 70, 84, 105, 140, 210 et 420.