Le but de ce sujet est de simuler la propagation d'un feu de forêt en fonction du vent. Le terrain est décrit par une carte carrée, représentée par une grille de cases.
Certaines de ces cases ne contiennent aucune matière combustible et sont donc des obstacles pour le feu. Ci-dessous à gauche, un exemple de carte où les cases grises représentent les obstacles, et la case jaune marquée d'un 0 représente le départ de feu.
 |
 |
Dans cette version du sujet, le feu se propage vers la gauche d'une case par jour, jusqu'au premier obstacle, comme représenté à droite.
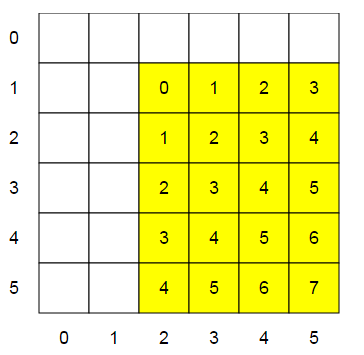
Dans cette version du sujet, la carte ne contient aucun obstacle et le feu se propage vers le bas et vers la droite, d'une case par jour. Exemple :
 |
 |
Dans cette version du sujet, le feu se propage vers le bas et vers la droite, d'une case par jour, jusqu'à rencontrer des obstacles, comme vous pouvez le voir dans l'illustration de droite.
 |
 |
Dans cette version du sujet, lLe feu se déplace dans les quatre directions (haut, bas, gauche, droite), d'une case par jour, jusqu'à rencontrer des obstacles. Pour l'exemple précédent, le résultat est représenté à droite ci-dessus : chaque case où le feu s'est propagé est en jaune et contient le numéro du jour où elle a commencé à brûler.
Votre objectif est d'écrire un programme qui indique à quelle date chaque case de la forêt suivante va brûler :

Pour cela, utilisez la fonction ecrireDate(lig, col, date), qui enregistre le fait que la case à la ligne et la colonne fournie en paramètres, va brûler à la date donnée. La fonction ne fait rien si la case se trouve en dehors du terrain.
Votre objectif est d'écrire un programme qui détermine à quelle date chaque case de la forêt va brûler.
Pour écrire votre programme, vous pouvez utiliser les fonctions suivantes :
- tailleCote() retourne le nombre de cases sur un côté de la zone carrée.
- ligDepart() retourne la ligne sur laquelle le feu commence à la date 0.
- colDepart() retourne la colonne sur laquelle le feu commence à la date 0.
- estObstacle(lig, col) retourne 1 si la case donnée est un obstacle qui ne brûle pas ou bien si la case se trouve en dehors du terrain, et retourne 0 sinon.
- ecrireDate(lig, col, date) enregistre le fait que la case donnée va brûler à la date donnée. (Ne fait rien si la case se trouve en dehors du terrain.)
- lireDate(lig, col) retourne la date qui a été enregistrée pour la case donnée, ou bien -1 si aucune date n'a été enregistrée. (Retourne -1 si la case se trouve en dehors du terrain.)
Comme indiqué sur les côtés de la grille, les lignes sont numérotées de 0 à 4 de haut en bas, et les colonnes sont numérotées de 0 à 4 de gauche à droite.
Les lignes sont numérotées de 0 à tailleCote()-1, de haut en bas, et les colonnes sont numérotées de 0 à tailleCote()-1, de gauche à droite.
Le feu se déclare initialement aux coordonnées (ligDepart(), colDepart()). Votre programme doit notamment appeler la fonction ecrireDate sur cette case de départ, en fournissant la date 0.
Exemple
Voici un programme qui propage le feu pendant 2 tours seulement :
Voici un programme qui propage le feu vers le bas jusqu'au premier obstacle :
Voici un programme qui met des départs de feu sur toutes les cases de la ligne ligDepart() qui ne sont pas des obstacles, puis propage le feu vers le bas jusqu'à rencontrer des obstacles ou le bord de la grille, à la vitesse d'une case par jour.
#include "lib.h"
int main() {
int taille = tailleCote();
int ligDep = ligDepart();
int colDep = colDepart();
for (int col = colDep; col < taille; col++) {
if (! estObstacle(ligDep, col))
ecrireDate(ligDep, col, 0);
}
for (int col = colDep; col < taille; col++) {
int date = lireDate(ligDep, col);
if (date != -1) {
int lig = ligDep;
while (! estObstacle(lig, col)) {
ecrireDate(lig, col, date);
lig++;
date++;
}
}
}
return 0;
}
#include "lib.h"
int main() {
int taille = tailleCote();
int ligDep = ligDepart();
int colDep = colDepart();
for (int col = colDep; col < taille; col++) {
if (! estObstacle(ligDep, col))
ecrireDate(ligDep, col, 0);
}
for (int col = colDep; col < taille; col++) {
int date = lireDate(ligDep, col);
if (date != -1) {
int lig = ligDep;
while (! estObstacle(lig, col)) {
ecrireDate(lig, col, date);
lig++;
date++;
}
}
}
return 0;
}
open Lib
let () =
let taille = tailleCote() in
let ligDep = ligDepart() in
for col = 0 to taille-1 do
if (estObstacle ligDep col) = 0 then begin
ecrireDate ligDep col 0;
end;
done;
for col = 0 to taille-1 do
let date = ref (lireDate ligDep col) in
if !date <> -1 then begin
let lig = ref ligDep in
while (estObstacle !lig col) = 0 do
ecrireDate !lig col !date;
lig := !lig + 1;
date := !date + 1;
done
end;
done
import static algorea.Lib.*;
class Main
{
public static void main(String[] args)
{
int taille = tailleCote();
int ligDep = ligDepart();
int colDep = colDepart();
for (int col = colDep; col < taille; col++) {
if (estObstacle(ligDep, col) == 0)
ecrireDate(ligDep, col, 0);
}
for (int col = colDep; col < taille; col++) {
int date = lireDate(ligDep, col);
if (date != -1) {
int lig = ligDep;
while (estObstacle(lig, col) == 0) {
ecrireDate(lig, col, date);
lig++;
date++;
}
}
}
}
}
import static algorea.Lib.*;
int taille = tailleCote();
int ligDep = ligDepart();
int colDep = colDepart();
for (int col = colDep; col < taille; col++) {
if (estObstacle(ligDep, col) == 0)
ecrireDate(ligDep, col, 0);
}
for (int col = colDep; col < taille; col++) {
int date = lireDate(ligDep, col);
if (date != -1) {
int lig = ligDep;
while (estObstacle(lig, col) == 0) {
ecrireDate(lig, col, date);
lig++;
date++;
}
}
}
from lib import *
taille = tailleCote()
ligDep = ligDepart()
for col in range(taille):
if not estObstacle(ligDep, col):
ecrireDate(ligDep, col, 0)
for col in range(taille):
date = lireDate(ligDep, col)
if date != -1:
lig = ligDep
while not estObstacle(lig, col):
ecrireDate(lig, col, date)
lig += 1
date += 1
Complétez ce programme pour qu'il propage le feu jusqu'au bout.
Modifiez ce programme pour qu'il propage le feu vers la gauche jusqu'au premier obstacle.
Ce programme n'a aucun rapport avec ce qui vous est demandé, mais vous rappelle comment faire des boucles imbriquées, et peut donc vous aider sur ce sujet.
Contraintes
Les données du problème vérifient les contraintes suivantes :
- 1 ≤ taille ≤ 20 où taille (le résultat de tailleCote()) décrit la taille d'un côté du terrain carré.
Tik užsiregistravę ir prisijungę galite pateikti šio uždavinio sprendimą.
Registravimasis užims vos keletą minučių, tuomet galėsite svetainėje spręsti uždavinius, juos testuoti bei pateikti jų sprendimus.
Prisijungę gausite iš anksto paruoštas užuominas arba galėsite kreiptis pagalbos į forumą.
Lorsque vous serez connecté(e), vous pourrez voir vos actions ici.
Une correction sera mise en ligne après la fin de l'épreuve.
 France-IOI
France-IOI
